Making Waves! - Detección de bordes

Este es el tercer artículo de una serie sobre shaders y ecuaciones diferenciales.

Anterior: Making Waves! - Desenfoque gaussiano

Siguiente: Making Waves! Ecuaciones diferenciales ordinarias

Detección de bordes

Se puede considerar un borde en una imagen el punto en el que la diferencia de colores cambia abruptamente. Si vemos a la imagen como una serie de Fourier, utilizando un filtro pasa bajos se pueden identificar los bordes. Mientras que un filtro pasa altos difumina la imagen.

En este artículo vamos a ver otro enfoque para la detección de bordes. Tomando la imagen como una función con dominio de dos dimensiones y considerando que los bordes mismos corresponden a grandes cambios de colores, se pueden estudiar los bordes con un poco de análisis matemático.


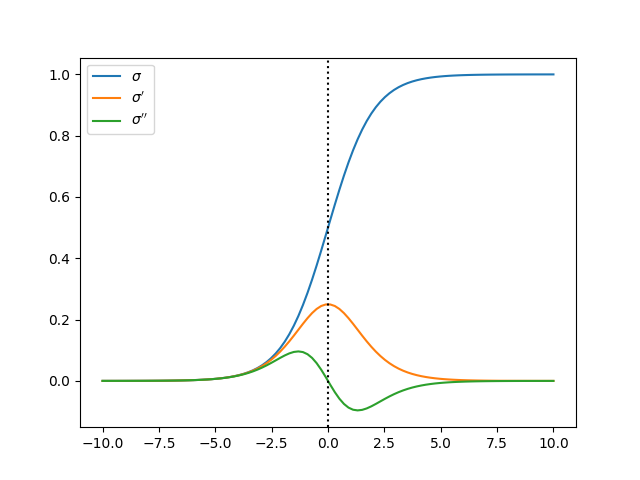
Figura 1: Función $\sigma$ en una dimensión y sus derivadas

En la Figura 1 se puede ver que cuando el color pasa de 0 a 1, un borde, la primer derivada muestra un pico y la segunda cruza el 0 hacia los negativos. Éstos conceptos ofrecen dos implementaciones de detección de bordes.

Detectar picos en la primer derivada
Detectar cruces de 0 en la segunda derivada: Zero Crossing Detector

El primero va a quedar como tarea para el hogar, en lo que resta del artículo vamos a armar un detector de cruces por cero.

Zero Crossing Detector

La base del detector es pasar la imagen por un filtro laplaciano. El filtro laplaciano está dado por la la operación laplaciana

\[L(x,y) = \frac{\partial^2 f(x,y)}{\partial^2 x} + \frac{\partial^2 f(x,y)}{\partial^2 y}\]

En cada pixel resultante se obtienen la suma de las segundas derivadas parciales en cada dirección. Informalmente, el operador laplaciano mide que tanto se desvía el valor de $f(x,y)$ con el promedio de su entorno.

Las primeras derivadas se pueden escribir:

\[\frac{\partial f(x,y)}{\partial x} = \lim_{h \to 0} \frac{f(x+h, y) - f(x, y)}{h}\] \[\frac{\partial f(x,y)}{\partial y} = \lim_{h \to 0} \frac{f(x, y+h) - f(x, y)}{h}\]

Y se pueden pensar como una diferencia de cocientes. Para calcular la segunda derivada, que es la diferencia de cocientes de la diferencia de cocientes, podemos aplicar la misma idea:

\[\frac{\partial^2 f(x,y)}{\partial^2 x} = \lim_{h \to 0} \frac{\frac{f(x+h, y) - f(x, y)}{h} - \frac{f(x, y) - f(x-h, y)}{h}}{h}\] \[\frac{\partial^2 f(x,y)}{\partial^2 y} = \lim_{h \to 0} \frac{\frac{f(x, y+h) - f(x, y)}{h} - \frac{f(x, y) - f(x, y-h)}{h}}{h}\] \[L(x,y) = \lim_{h \to 0} \frac{f(x, y+h) + f(x-h, y) + f(x, y+h) + f(x, y-h) - 4f(x,y)}{h^2}\]

El problema que surge ahora es que la imagen no es una función continua, por lo que no podemos calcular la derivada analíticamente. Lo que se suele hacer es aproximar, hacer de cuenta que los pixeles están unidos por una recta. Si fijamos $h=1$, la formula aproximada es:

\[L(x,y) \approx f(x, y+1) + f(x-1, y) + f(x, y+1) + f(x, y-1) - 4f(x,y)\]

Y, viendolo desde otro ángulo, el filtro laplaciano es lo mismo que aplicar una convolución a la imagen con el kernel:

\[\begin{bmatrix} 0 & 1 & 0 \\ 1 & -4 & 1 \\ 0 & 1 & 0 \end{bmatrix}\]

Imagen resultante de la convolución con el kernel laplaciano.
Dado que los valores resultantes no son entre 0 y 1, se normalizaron para que lo sean.

Zero Crossing

Hay varias maneras de detectar un cruce por cero. Algo a tener en cuenta es que como estamos trabajando con funciones no continuas, es muy posible que no haya pixeles en donde el valor sea $0$.

La siguiente matriz fue extraída de una imagen con un filtro laplaciano.

\[\begin{bmatrix} 9 & 19 & 21 \\ 18 & 21 & 24 \\ -13 & -10 & -5 \\ \end{bmatrix}\]

Parece haber un cruce por cero entre las ultimas dos filas, pero ningun valor es 0. Podemos considerar un un pixel $(i,j)$ con valor $f(i,j)$ como cruce si:

$f(i,j) \geq 0$
Algún vecino $(x,y)$ cumple $f(x,y) < 0$ y $f(i,j)-f(x,y) < \delta$

Solo se consideran bordes cuando los pixeles positivos cruzan a los negativos, y cuando la diferencia con el vecino supera determinado $\delta$. Si se quisiera aproximar un poco mejor, se puede tomar como borde al pixel más cercano a $0$ al momento del cambio de signo. El $\delta$ existe por el ruido en la imagen, si no se usa, cualquier cambio de color por más chico que sea se considera un borde. Una vez determinados los bordes, los pintamos con algun color y pintamos el resto de otro. Lo más común es utilizar $255$ y $0$.


Zero Crossing con $\delta = 0$	Zero Crossing con $\delta = 0.1$

LoG

Una técnica que se suele utilizar para esquivar el ruido en la imagen es pasarla previamente por un filtro gaussiano. Este filtro suaviza las irregularidades y mejora en general el funcionamiento de detección de bordes. Al laplaciano aplicado luego de una gaussiana, lo llamamos Laplacian of Gaussian, o LoG.


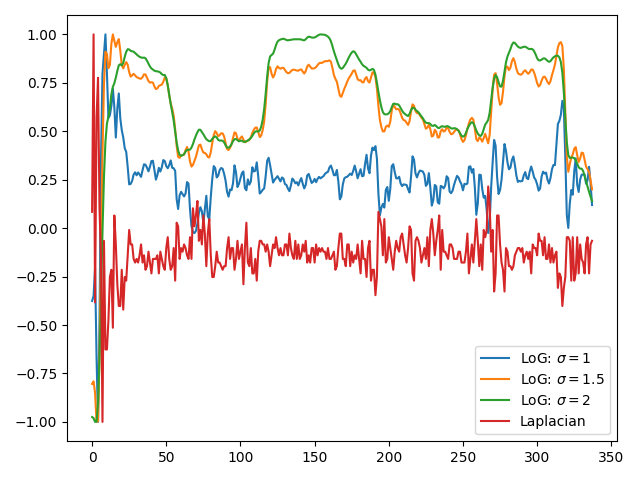
Figura 2: Comparación de convolución Laplaciana con LoG

En la Figura 2 se hace una comparación de una sola fila de píxeles de una imagen con distintos filtros aplicados. Mientras más suave sea el filtro gaussiano, más suave se hace la linea de píxeles.

Una manera de computar este nuevo filtro es primero pasar la imagen por el desenfoque gaussiano y luego por el laplaciano. Por suerte, las convoluciones son asociativas y conmutativas, por lo que se puede simplificar la operación.

\[L * (G * f) = (L * G) * f = f * (L * G) = f * LoG\]

$L$ es el kernel laplaciano, $G$ es el kernel gaussiano, $f$ es la imagen original y $*$ es el operador de convolución.

Esto significa que podemos tomar el laplaciano de la gaussiana y dejarlo fijo, luego usarlo como kernel para filtrar imágenes. Para tener una mejor aproximación, podemos calcular el laplaciano de la gaussiana analíticamente ¹.

\[G(x,y) = e^{-\frac{x^2+y^2}{2\sigma^2}}\] \[\frac{\partial G(x,y)}{\partial x} = -\frac{x}{\sigma^2}G(x,y)\] \[\frac{\partial^2 G(x,y)}{\partial^2 x} = (\frac{x^2}{\sigma^4}-\frac{1}{\sigma^2})G(x,y)\] \[LoG(x,y) = \frac{\partial^2 G(x,y)}{\partial^2 x} + \frac{\partial^2 G(x,y)}{\partial^2 y} = (\frac{x^2 + y^2}{\sigma^4} - \frac{2}{\sigma^2})G(x,y)\]

Aplicando la misma idea que para el desenfoque gaussiano podemos generar una convolución.

import numpy as np

def gaussian2d(x, y, sig):
    return np.exp(-(x**2 + y**2) / (2 * sig**2)) / (2 * np.pi * sig**2)

def log_2d(x,y,sigma):
    return ((x**2 + y**2)/sigma**4 - 2/sigma**2)*gaussian2d(x,y,sigma)

def kernel_log_2d(size, sigma):
    kernel = np.fromfunction(lambda x, y: log_2d(x - size // 2, y - size // 2, sigma), (size, size))
    kernel *= 100/np.min(kernel)
    kernel = np.round(kernel, 0)
    return kernel

# Genero un kernel gaussiano de 7x7 con sigma 1
print(kernel_log_2d(7, 1))

Kernel LoG con $\sigma = 1$, $7x7$

$$\begin{bmatrix} -0 & -1 & -3 & -4 & -3 & -1 & -0 \\ -1 & -5 & -12 & -14 & -12 & -5 & -1 \\ -3 & -12 & -0 & 30 & -0 & -12 & -3 \\ -4 & -14 & 30 & 100 & 30 & -14 & -4 \\ -3 & -12 & -0 & 30 & -0 & -12 & -3 \\ -1 & -5 & -12 & -14 & -12 & -5 & -1 \\ -0 & -1 & -3 & -4 & -3 & -1 & -0 \\ \end{bmatrix}$$

Idealmente el kernel de convolución debería ser tan grande como información aporta $LoG$, es decir, cortar cuando los valores sean muy cercanos a $0$. Mientras incrementa el valor $\sigma$, más se aplana la gaussiana y menos bordes se van a encontrar.

El siguiente gráfico muestra como varía LoG en base a $\sigma$ y como esto afecta el resultado con $\delta = 0$.

Fijando $\sigma = 1.4$ se puede jugar con $\delta$.²

El código para generar los gráficos lo pueden ver en el notebook. Lamentablemente todavía no preparé el servidor estático para que muestre notebooks de manera feliz.

Pudimos ver como con análisis de derivadas podemos obtener un insight interesante de las features de una imagen. En el siguiente artículo vamos a ver como estas ideas se relacionan con cambios a través del tiempo.

Anterior: Making Waves! - Desenfoque gaussiano

Siguiente: Making Waves! - Ecuaciones diferenciales ordinarias

Lecturas recomendadas y referencias:

Traté de encontrar la justificación por la cual se puede hacer esto, dado que calcular el laplaciano no es aplicar la convolución. ↩
Estuve una cantidad de tiempo absurdo tratando de encontrar animaciones que pudiera pasar a html facil. Terminé utilizando plotly y no pude incluir dos sliders en la misma animación. ↩