Making Waves! - Desenfoque gaussiano
Este es el segundo artículo de una serie sobre shaders y ecuaciones diferenciales.
Anterior: Making Waves! Rotación RGB
Siguiente: Making Waves! Detección de bordes
Desenfoque gaussiano
El desenfoque gaussiano es una técnica utilizada en procesamiento de imágenes para suavizar o difuminar una imagen. Lo hace promediando el valor de los pixeles en relación a su entorno.
 |
 |
| Imagen Base | Desenfoque gaussiano |
Asumiendo una imagen en blanco y negro, se puede modelar como una matriz \(m\) de dimensiones \(WxH\) en donde \(m_{ij}\) es un valor entre 0 y 1 que define que tan negro es el pixel en la posición \((i,j)\).
Una posibilidad para promediar el valor de pixel \(m_{ij}\) puede ser promediar en un rango de 3x3 para generar el filtro de difuminación Box Blur.
\[\begin{bmatrix} m_{11} & m_{12} & \dots & \dots & \dots & \dots & \dots & m_{1W} \\ m_{21} & m_{22} & \dots & \dots & \dots & \dots & \dots & m_{2W} \\ \dots & \dots & \dots & \dots & \dots & \dots & \dots \\ m_{(i-1)1} & m_{(i-1)2} & \dots & \color{red}{m_{(i-1)j}} & \color{red}{m_{i(j+1)}} & \color{red}{m_{(i+1)(j-1)}} & \dots & m_{(i-1)W} \\ m_{i1} & m_{i2} & \dots & \color{red}{m_{i(j-1)}} & \color{red}{m_{ij}} & \color{red}{m_{i(j-1)}} & \dots & m_{iW} \\ m_{(i+1)1} & m_{(i+1)2} & \dots & \color{red}{m_{(i+1)j}} & \color{red}{m_{(i+1)(j-1)}} & \color{red}{m_{(i+1)(j+1)}} & \dots & m_{(i+1)W} \\ \dots & \dots & \dots & \dots & \dots & \dots & \dots & \dots \\ m_{H1} & m_{H2} & \dots & \dots &\dots & \dots & \dots & m_{HW} \\ \end{bmatrix}\]El nuevo pixel promediado se puede calcular como la suma del entorno dividido la cantidad de elementos:
\[dg(i,j) = \frac{1}{9}\sum_{i'=i-1}^{i+1}\sum_{j'=j-1}^{j+1} m_{i'j'}\]La operación \(dg\) no se encuentra definida para los bordes de la imagen, hay varias maneras para manejar esta situación y como estamos diseñando nuestro propio filtro, podemos elegir lo que queramos, por ejemplo, dejar el pixel como está.
\[\forall i, dg(i,0) = m_{i0}\] \[\forall j, dg(0,j) = m_{0j}\]Podemos jugar con esta idea de promediar pixeles en relación a su entorno, por ejemplo, no usar un promedio ponderado. Se puede definir una función y tomar promedios en los que los pixeles más cercanos al valor que queremos tengan un peso mayor. Cuando la función elegida es gaussiana, estamos hablando de un desenfoque gaussiano.
| \(G(x,y) = \frac{1}{2\pi\sigma^2}e^{-\frac{x^2+y^2}{2\sigma^2}}\) |
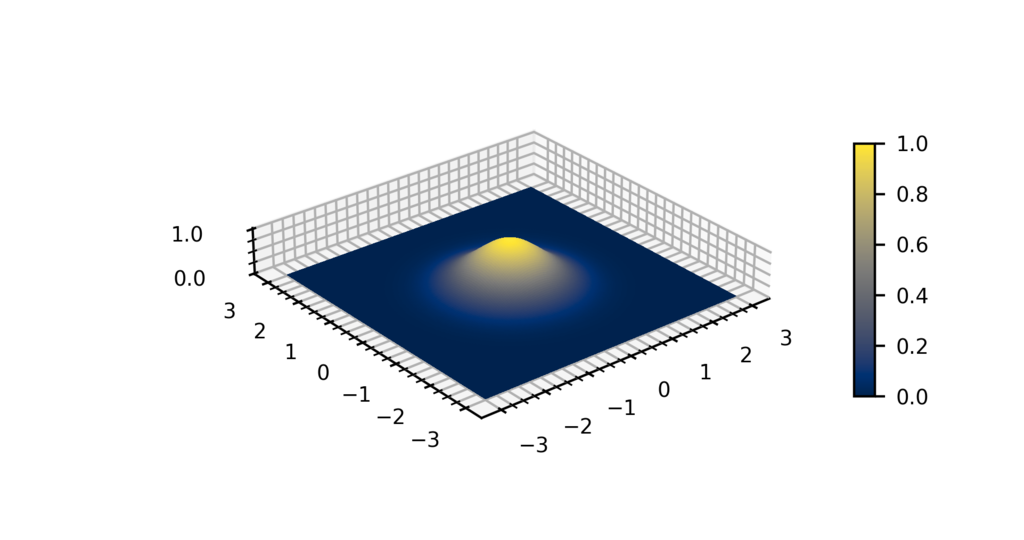 |
| Gráfico en 3d de la función gaussiana en dos dimensiones. \(\sigma\) define que tan aplanado es el resultado. |
Antes de seguir, es útil entender el concepto de convolución para ver una generalización de esta idea.
Convolución
La convolución es una operación matemática, una especie de media móvil en la que se agrupan y promedian conjuntos de puntos. En el caso del desenfoque gaussiano, se aplica un kernel gaussiano a cada píxel de la imagen, calculando el promedio ponderado de los valores de los píxeles vecinos.
El kernel gaussiano es una matriz de valores que sigue una distribución gaussiana. Los valores del kernel determinan la cantidad de desenfoque aplicado a la imagen. Cuanto mayor sea el valor del kernel en el centro y más pequeños sean los valores en los bordes, mayor será el efecto de desenfoque.
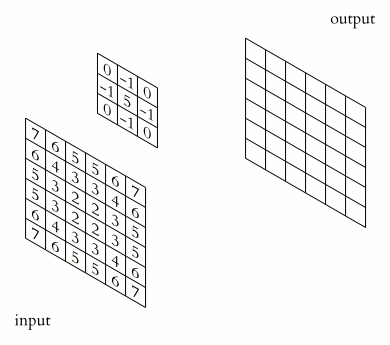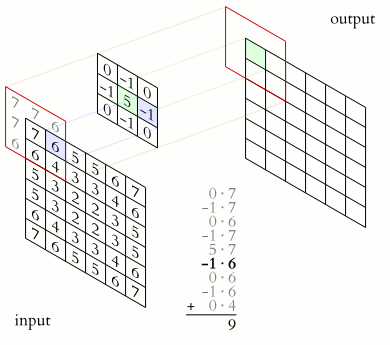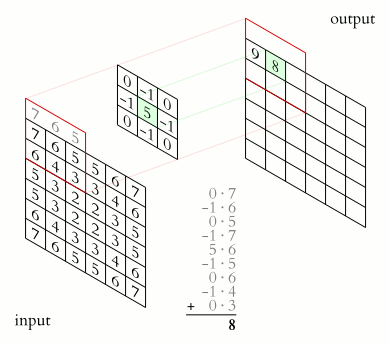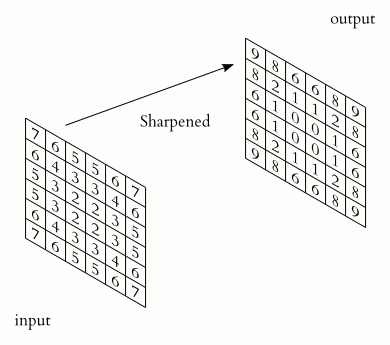 |
Proceso de convolución de imagen con kernel |
En el caso de Box Blur el kernel a que utilizamos esta dado por la matriz:
\[\begin{bmatrix} 1/9 & 1/9 & 1/9 \\ 1/9 & 1/9 & 1/9 \\ 1/9 & 1/9 & 1/9 \end{bmatrix}\]Para que estemos tomando un promedio efectivamente, la suma de todos los elementos tiene que dar 1. Pero se puede jugar con otros valores y ver que pasa.
Kernel de desenfoque gaussiano
Considerando convoluciones, sólo queda plantear una matriz para representar un promedio gaussiano. Para lograrlo, consideremos la función gaussiana en dos dimensiones \(G(x,y)\), \(\sigma = 1\) y un kernel de \(3x3\). Idealmente, el centro del kernel debería coincidir con el centro de la gaussiana e ir aplanandose hacia los bordes, por ejemplo el kernel.
\[\begin{bmatrix} G(-1,-1) & G(0,-1) & G(1,-1) \\ G(-1,0) & G(0,0) & G(1,0) \\ G(-1,1) & G(0,1) & G(1,1) \end{bmatrix} = \begin{bmatrix} 0.059 & 0.097 & 0.059 \\ 0.097 & 0.159 & 0.097 \\ 0.059 & 0.097 & 0.059 \end{bmatrix}\]El problema es que la matriz resultante no suma 1, eso va a hacer que luego de aplicarlo la imagen tienda a ser más oscura. Hay muchas maneras de solucionar este problema, por ejemplo, dividir cada valor por la suma de la matriz. Personalmente, me gusta que los valores de la matriz sean enteros para poder representarla más fácil. El siguiente código de python genera kernels gaussianos de distintos tipos
import numpy as np
def gaussian2d(x, y, sig):
return np.exp(-(x**2 + y**2) / (2 * sig**2)) / (2 * np.pi * sig**2)
def gaussian2d_kernel(size, sig):
kernel = np.fromfunction(lambda x, y: gaussian2d(x - size // 2, y - size // 2, sig), (size, size))
# Multiplico toda la matriz para que el valor más chico sea 1
kernel *= 1/np.min(kernel)
# Redondeo para tener solo enteros
return np.round(kernel, 0)
# Genero un kernel gaussiano de 3x3 con sigma 1
print(gaussian2d_kernel(3, 1))
| Parámetros | Kernel |
|---|---|
| \(3x3, \sigma = 1\) | $$\frac{1}{15}\begin{bmatrix} 1 & 2 & 1 \\ 2 & 3 & 2 \\ 1 & 2 & 1 \end{bmatrix}$$ |
| \(5x5, \sigma = 1\) | $$\frac{1}{331}\begin{bmatrix} 1 & 4 & 7 & 4 & 1 \\ 4 & 20 & 33 & 20 & 4 \\ 7 & 33 & 55 & 33 & 7 \\ 4 & 20 & 33 & 20 & 4 \\ 1 & 4 & 7 & 4 & 1 \\\end{bmatrix}$$ |
| \(5x5, \sigma = 0.9\) | $$\frac{1}{704}\begin{bmatrix} 1 & 6 & 12 & 6 & 1 \\ 6 & 41 & 75 & 41 & 6 \\ 12 & 75 & 140 & 75 & 12 \\ 6 & 41 & 75 & 41 & 6 \\ 1 & 6 & 12 & 6 & 1 \\ \end{bmatrix}$$ |
En el siguiente artículo vamos a ver cómo este tipo de operaciones puede utilizarse para detectar bordes con un poco de análisis matemático
Anterior: Making Waves! Rotación RGB
Siguiente: Making Waves! Detección de bordes